What Size Are Hexagons In Official Soccer Ball

This Commodity From Issue

July-Baronial 2006

Volume 94, Number 4

With the arrival of the quadrennial soccer Globe Cup this summer, more than a billion people around the world are finding their television and estimator screens filled with depictions of soccer balls. In Frg, where the World Cup matches are being played, soccer balls are turning up on all kinds of merchandise, much of it having nothing to practice with soccer.

Figure 1. Twelve pentagons and 20 hexagons form a figure known to mathematicians as a truncated icosahedron, to chemists as the buckminsterfullerene molecule—and to well-nigh everybody else every bit the standard soccer ball. Every bit this summer's World Loving cup competition approached, a soccer ball-shaped information pavilion toured the German cities preparing to host Earth Loving cup matches. Here the "football globe" makes a finish in Leipzig. The iconic black and white soccer ball is also an intriguing puzzle amenable to mathematical analysis. Other soccer assurance that may never be seen on the playing field also offer interesting solutions to the mathematical questions posed by the standard pattern.

Sabina Sarnitz/GmbH

Although a soccer ball can exist put together in many different ways, there is one design so ubiquitous that it has become iconic. This standard soccer ball is stitched or glued together from 32 polygons, 12 of them v-sided and 20 six-sided, bundled in such a way that every pentagon is surrounded by hexagons. Postmodern paint jobs notwithstanding, the traditional way to color such a brawl is to paint the pentagons blackness and the hexagons white. This colour scheme was reportedly introduced for the World Loving cup in 1970 to enhance the visibility of the ball on television, although the design itself is older.

Most people associate the soccer-ball paradigm with hours spent on the field or the sidelines, or perhaps just with advertisements for sport merchandise. Merely to a mathematician, a soccer ball is an intriguing puzzle. Why does information technology wait the fashion it does? Are there other ways of putting it together? Could the pentagons and hexagons be arranged differently? Could other polygons be used instead of pentagons and hexagons? These questions tin can be tackled using the language of mathematics—in particular geometry, group theory, topology and graph theory. Each of these subjects provides concepts and a natural context for phrasing questions such every bit those about the blueprint of soccer balls, and sometimes for answering them as well.

An of import aspect of the awarding of mathematics is that different means of making mathematical sense of everyday questions lead to different answers. This may come equally a bit of a surprise to readers who are used to schoolbook problems that accept only one right answer. Properly framing questions is only as of import a part of the art of mathematics as answering them. Moreover, a genuine mathematical exploration of an open-concluded question does not stop with finding "the answer" (if in that location is one), but involves understanding why the answer is what it is, and how it changes when the underlying assumptions are modified. The questions posed past the pattern of soccer assurance provide a wonderful analogy of this process.

Mathematicians like to begin by defining their terms. What, and so, is a soccer ball? An official soccer ball, to be approved past the Fédération Internationale de Football Association (FIFA), must exist a sphere with a circumference between 68 and 70 centimeters, with at most a ane.5 percent divergence from sphericity when inflated to a force per unit area of 0.8 atmospheres.

Figure 2. Soccer-ball design over the years has been driven by the need for a round brawl that holds its shape and by the engineering science available. Eight panels of vulcanized rubber were glued together to create the ball at left, used in the primeval soccer championship in the Us in 1863. The leather ball at center, used in the 1950 World Cup, has a design typical of its era. The small number of large, irregularly shaped flat pieces adversely affected its roundness. Thank you to improvements in materials and manufacturing, curved pieces in more complicated shapes can now exist used. This year'southward World Loving cup ball (right) is made from 14 synthetic-leather panels cut in intricately curved shapes. In graph-theory terms, this ball is a truncated octahedron.

Historic photographs courtesy of Jack Huckel, National Soccer Hall of Fame; correct photograph courtesy of firosportfoto.de.

Alas, such a definition says naught about how the ball is put together, and is therefore non suitable for a mathematical exploration of the pattern. A better definition is that a soccer brawl is approximately a sphere fabricated of polygons, or what mathematicians phone call a spherical polyhedron. The places where the polygons come together—the vertices and edges of the polyhedron—trace out a map on the sphere, which is called a graph. (Such a graph has nothing to practice with graphs of functions. The word has two completely different mathematical meanings.) Examined from the perspective of graph theory, the standard soccer brawl has three of import properties:

(one) it is a polyhedron that consists merely of pentagons and hexagons;
(two) the sides of each pentagon meet simply hexagons; and
(3) the sides of each hexagon alternately meet pentagons and hexagons.

As a starting point, then, we can define a soccer ball to be any spherical polyhedron with properties (1), (2) and (3). If the pentagons are painted black and the hexagons are painted white, then the definition does capture the iconic epitome, though it does not determine it uniquely.

This definition places the problem of soccer ball design into the context of graph theory and topology. Topology, often described equally "rubber-sheet geometry," is the co-operative of mathematics that studies properties of objects that are unchanged by continuous deformations, such as the inflation of a soccer ball. For the purposes of topology, it doesn't matter how long the edges of a polyhedron are, or whether we are dealing with a round polyhedron or 1 with apartment sides.

I commencement encountered the above definition in 1983, in a trouble posed in the Bundeswettbewerb Mathematik, a High german mathematics competition for loftier school students. The problem was: Given properties (i)-(3), determine how many pentagons and hexagons a soccer ball is made of. Thinking about this problem at the time, I assumed that the ball is a convex polyhedron in infinite made upwardly of regular polygons. This geometric assumption, together with rules (one), (2) and (three), implies that there are 12 pentagons and 20 hexagons. Moreover, there is a unique style of putting them together, giving ascension to the iconic standard soccer ball. Without the geometric assumption, the graph-theory problem has infinitely many other solutions, which have larger numbers of pentagons and hexagons.

I began thinking well-nigh this problem again later on I was invited to give a lecture at a prize ceremony for the same competition in 2001. Eventually, 1 of my postdoctoral fellows, Volker Braungardt, and I establish a way to characterize all the solutions, a label that I will draw beneath.

Figure 3. Fullerenes are large carbon molecules whose shapes are made up of pentagons and hexagons that come across three at a time, in such a way that no two pentagons are adjacent. Every fullerene contains exactly 12 pentagons, merely at that place is no limit to the number of hexagons. The simplest fullerene molecule, C60, has the iconic soccer-ball shape. Other fullerenes, such every bit C80, have been made in the laboratory. Mathematically, the combinatorics of fullerenes is an awarding of Euler's formula.

Aaron Cox, adjusted from drawings by Riichiro Saito in Dresselhaus et al. 1996

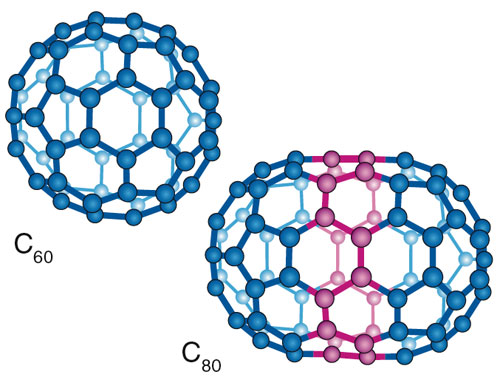
Interestingly, a related problem arose in chemistry in the 1980s after the 60-cantlet carbon molecule, called the buckminsterfullerene or "buckyball," was discovered. The spatial shape of this C_threescore molecule is identical to the standard soccer-ball polyhedron consisting of 12 pentagons and 20 hexagons, with the threescore carbon atoms placed at the vertices and the edges corresponding to chemic bonds. The discovery of the buckyball, which was honored past the 1996 Nobel Prize for chemical science, created enormous interest in a class of carbon molecules chosen fullerenes, which satisfy assumption (1) above together with a further status:

(3') precisely iii edges meet at every vertex.

This property is forced by the chemical bonding properties of carbon. In addition, assumption (2) is sometimes imposed to define a restricted form of fullerenes. Having disjoint pentagons is expected to exist related to the chemic stability of fullerenes. At that place are infinitely many fullerene polyhedra—C_lx was merely the commencement one discovered as an bodily molecule—and it is quite remarkable that the two infinite families of polyhedra, the soccer assurance and the fullerenes, have only the standard soccer brawl in common. Thus (one)-(3) together with (three¢) give a unique clarification of the standard soccer ball without imposing geometric assumptions. (Assumptions like regularity in fact imply condition (three¢).)

To see that this is so requires a brief circuit into properties of polyhedra, starting with a beautiful formula discovered by the Swiss mathematician Leonhard Euler in the 18th century. Euler's formula (come across "Euler's formula," beneath), a basic tool in graph theory and topology, says that in any spherical polyhedron, the number of vertices, v, minus the number of edges, e, plus the number of faces, f, equals 2:

v - due east + f = ii

Permit'due south apply Euler'due south formula to a polyhedron consisting of b black pentagons and w white hexagons. The total number f of faces is b + westward. In all, the pentagons have 5b edges, because there are v edges per pentagon and b pentagons in all. Similarly, the hexagons have a total of 6w edges. Adding these two numbers should give the total number of edges—except that I accept counted each border twice because each edge lies in two different faces. To compensate I separate by 2, and hence the number of edges is:

e = (1/ii )(5b + 6w)

Finally, to count the number of vertices, I note that the pentagons have 5b vertices in all and the hexagons have 6w vertices. In the example of a fullerene, assumption (3¢) says that each vertex belongs to 3 different faces. Thus if I compute 5b + 6w, I have counted each vertex exactly iii times, and hence I must separate by 3 to compensate:

v = (ane/3)(5b + 6w)

Substituting these values for f, e and v into Euler's formula, I find that the terms involving w abolish out, and the formula reduces to b = 12. Every fullerene, therefore, contains exactly 12 pentagons! However, there is no a priori limit to the number of hexagons, w, and therefore no limit on the number of vertices. (This is implicit in the title of a 1997 article on fullerenes in American Scientist: "Fullerene Nanotubes: C_1,000,000 and Beyond.") If I impose the additional status (2), then I tin can bear witness that the number of hexagons has to be at least 20. The standard soccer ball or buckyball realizes this minimum value, for which the number v of vertices equals 60, corresponding to the 60 atoms in the C₆₀ molecule. However, it can exist shown that there are indeed infinitely many other mathematical possibilities for fullerene-shaped polyhedra. Which of these represent to bodily molecules is a subject of research in chemistry.

For soccer assurance, we are immune to utilize only assumptions (ane)-(iii), merely not (three¢), the carbon chemist's requirement that three edges meet at every vertex. In this case the number of faces meeting at a vertex is not fixed, but this number is at least 3. Therefore, the equation v = (1/3)(5b + 6w) becomes an inequality: v £ (1/3)(5b + 6w). Substituting into Euler's formula, the terms involving w once more cancel out, leaving the inequality b ³ 12. Thus every soccer ball contains at least 12 pentagons, simply, dissimilar a fullerene, may well contain more.

Also unlike fullerenes, soccer balls have a precise relation between the number of pentagons and the number of hexagons. Counting the number of edges along which pentagons and hexagons meet, condition (2) says that all edges of pentagons are also edges of hexagons, and condition (3) says that exactly half of the edges of hexagons are also edges of pentagons. Hence (1/2)(6w) = 5b, or 3w = 5b. Because b ³ 12, w is at least 20. These minimal values are realized by the standard soccer brawl, and the realization is combinatorially unique considering of atmospheric condition (2) and (iii). But there are also infinitely many other numerical solutions, and the trouble arises whether these non-minimal numerical solutions stand for to soccer-ball polyhedra. It turns out that they do, every bit we'll see shortly, then that there is indeed an infinite drove of soccer assurance.

Thus we see that at that place are infinitely many fullerenes (satisfying assumptions (i), (2) and (3¢)) and infinitely many soccer assurance (satisfying (1), (2) and (3)). Nevertheless, if we combine the two definitions, there is but one possibility! For a fullerene, b = 12, and for a soccer ball, 5b = 3w. Consequently, for a soccer brawl to likewise be a fullerene, nosotros must conclude that five ´ 12 = 3w, or w = 20. Any soccer ball that is also a fullerene must therefore accept 12 pentagons and 20 hexagons. It is known that there are 1,812 distinct fullerenes with 12 pentagons and 20 hexagons, but one,811 of them have side by side pentagons somewhere and are therefore not soccer balls, because they violate condition (2). The standard soccer ball is the only i with no adjacent pentagons.

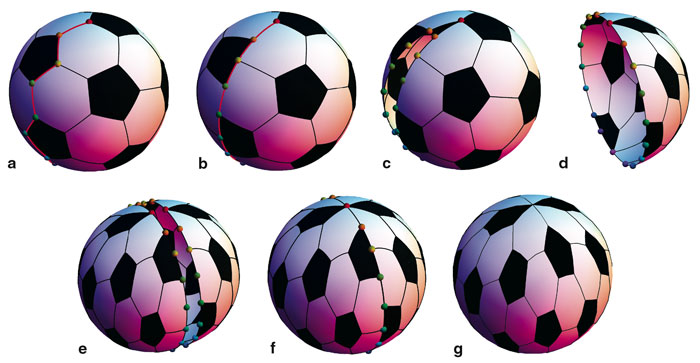
Leaving behind chemistry and fullerene graphs, permit us now consider the crucial question: What other, nonstandard, soccer balls are in that location, with more than three faces meeting at some vertex, and how tin can nosotros understand them? It turns out that we can generate infinite sequences of different soccer balls by a topological construction chosen a branched covering. You tin can visualize this by imagining the standard soccer-ball pattern superimposed on the surface of the Earth and aligned so that there is ane vertex at the N Pole and one vertex at the South Pole. Now distort the pattern so that one of the zigzag paths forth edges from pole to pole straightens out and lies on a meridian, say the prime meridian of zero geographical longitude (see Figure 4b). Information technology is all correct to distort the graph, because we are doing "prophylactic-canvas geometry."

Figure iv. New soccer balls tin be made from existing ones by a mathematical construction called a branched roofing. First ane chooses a seam of the onetime soccer ball along the edges of polygons (a). This seam is straightened out and sliced open (b, c). The whole surface of the soccer ball is shrunk to encompass just a hemisphere (d). A second copy of this hemisphere is rotated around and stitched to the outset (e, f). This builds a new soccer ball, which tin exist deformed equally in g. Conforming to the definition of a soccer brawl, black faces in the new ball are adjacent to only white faces (faces that meet just at vertices are non considered side by side), and white faces have an alternate sequence of white and black faces around their edges.

Soccer-ball images were calculated and created by Michael Trott using Mathematica.

Side by side, imagine slicing the World open up along the prime meridian. Shrink the sliced-open coat of the Earth in the e-w direction, belongings the poles fixed, until the coat covers exactly half the sphere, say the Western Hemisphere. Finally, take a copy of this shrunken coat and rotate it around the n-southward axis until it covers the Eastern Hemisphere. Remarkably, the two pieces can be sewn together, giving the sphere a new construction of a soccer brawl with twice as many pentagons and hexagons as before. The reason is that at each of the two seams running between the North and Southward Poles, the two sides of the seam are duplicate from the two sides of the cutting we made in our original soccer brawl. Therefore, the two pieces fit together perfectly, in such a way that the adjacency conditions (2) and (3) are preserved. (See Figure 4 for step-by-step illustrations of this construction.)

Effigy five. Infinitely many soccer assurance can exist constructed past the method used in Figure 4. For example, an eight-fold branched roofing of the standard soccer brawl can be built by using 8 copies of the sliced-open coat of the standard brawl to create a soccer ball with 96 pentagons and 160 hexagons. The eight pieces fit together like sections of an orange. The author and his collaborator Volker Braungardt have proved that every soccer ball is a branched covering of the standard i.

Soccer-ball images were calculated and created past Michael Trott using Mathematica.

The new soccer ball synthetic in this way is chosen a two-fold branched covering of the original i, and the poles are called branch pointsouthward. The new ball looks the same as the old i (from the topological or rubber-canvas geometry signal of view), except at the branch points. There are now half-dozen faces (instead of three) meeting at those 2 vertices, and there are 116 other vertices (the 58 vertices that weren't pinned at the poles, plus their duplicates), with three faces meeting at each of them.

Figure vi. The proof that branched coverings produce all soccer balls depends on an assay of the sequence of colors effectually whatsoever vertex. Because at to the lowest degree one of the edges meeting at each vertex bounds a pentagon (blackness), at that place is no vertex where but hexagons (white) meet. The sequence of faces around a vertex is always black-white-white, blackness-white-white, and closes upwards later a number of faces that is a multiple of iii.

SIGANIM/Spektrum de Wissenschaft and Michael Trott

At that place is a straightforward modification we can make to this construction. Instead of taking 2-fold coverings, we tin take d-fold branched coverings for any positive integer d. Instead of shrinking the sphere halfway, nosotros imagine an orange, made up of d orangish sections, and for each section nosotros shrink a copy of the coat of the sphere and then that it fits precisely over the department. Once once again the unlike pieces fit together forth the seams (run across Figure 5). For all of this it is important that we think of soccer assurance as combinatorial or topological—not geometric—objects, so that the polygons can be distorted arbitrarily.

At this point yous might think that there could be many more examples of soccer assurance, perhaps generated from the standard i by other modifications, or perhaps sporadic examples having no apparent connexion to the standard soccer ball. Just this is not the instance! Braungardt and I proved that every soccer ball is in fact a suitable branched roofing of the standard one (maybe with slightly more than complicated branching than was discussed above).

The proof involved an interesting interplay between the local structure of soccer balls around each vertex and the global construction of branched coverings. Consider whatsoever vertex of any soccer ball (see Effigy half-dozen). For every face up meeting this vertex, there are 2 consecutive edges that meet at that place. Because at least one of those two edges bounds a pentagon, by condition (iii), there is no vertex where only hexagons meet. Thus at every vertex at that place is a pentagon. Its sides meet hexagons, and the sides of the hexagons alternately meet pentagons and hexagons. This condition can be met simply if the faces are ordered around the vertex in the sequence black, white, white, black, white, white, etc. (Remember that the pentagons are blackness.) In club for the design to close up around the vertex, the number of faces that meet at this vertex must be a multiple of 3. This means that locally, around any vertex, the construction looks just like that of a branched roofing of the standard soccer ball around a branch point. Covering infinite theory—the part of topology that investigates relations between spaces that look locally alike—so enabled usa to prove that any soccer brawl is in fact a branched covering of the standard one.

To mathematicians, generalization is second nature. Even later on something has been proved, it may non be apparent exactly why information technology is true. Testing the argument in slightly unlike situations while probing generalizations is an important role of really agreement information technology, and seeing which of the assumptions used are essential, and which can be dispensed with.

A quick await at the arguments above reveals that there is very fiddling in the assay of soccer balls that depends on their beingness fabricated from pentagons and hexagons. So it is natural to define "generalized soccer balls" allowing other kinds of polygons. Imagining that we again color the faces black and white, we assume that the blackness faces accept k edges, and the white faces accept 50 edges each. For conventional soccer assurance, thou equals five, and l equals half-dozen. As before, the edges of black faces are required to run across only edges of white faces, and the edges of the white faces alternately meet edges of black and white faces. The alternation of colors forces l to be an even number.

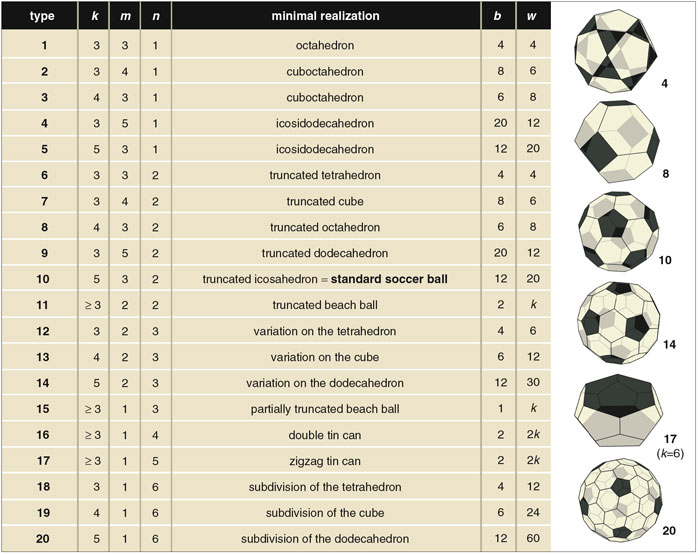
Going one step further in this process of generalization, nosotros can require that every nth edge of a white face meets a blackness face, and all its other edges encounter white faces. This forces l to be a multiple of n; that is, l = m ´n for some integer m. Of course we nevertheless require that the edges of black faces run into only white faces. Let u.s.a. phone call such a polyhedron a generalized soccer ball. Thus the design of a generalized soccer brawl is described by the three integers (grand, m, n), where k is the number of sides in a black face, l = m ´ n is the number of sides in a white face up, and every nth side of a white face meets a black face. The first question we must ask is: Which combinations of k, m and due north are actually possible for a generalized soccer ball? It turns out that the answer to this question is closely related to the regular polyhedra.

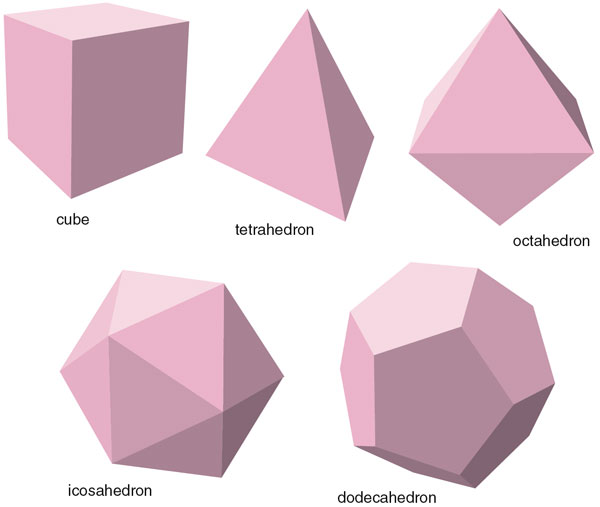
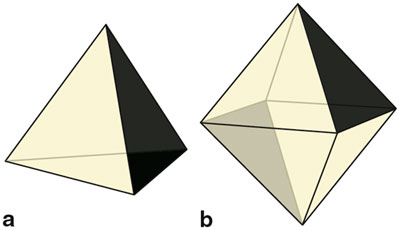
Ancient Greek mathematicians and philosophers were fascinated past the regular polyhedra, also known as Platonic solids, attributing to them many mystical backdrop. The Platonic solids are polyhedra with the greatest possible degree of symmetry: All their faces are equilateral polygons with the aforementioned number of sides, and the same number of faces run into at every vertex. Euclid proved in his Elements that there are only five such polyhedra: the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron (run across Figure 7).

Effigy 7. The five bones Platonic solids shown here accept been known since antiquity. Examples of all generalized soccer-ball patterns can be generated by altering Platonic solids.

SIGANIM/Spektrum de Wissenschaft

Although Euclid used the geometric definition of Platonic solids, assuming all the polygons to be regular, modernistic mathematicians know that the argument does non depend on the geometry. In fact, a topological statement using only Euler'southward formula shows that there are no possibilities other than the 5 shown in Figure 7.

Each Ideal solid tin can exist described by two numbers: the number Grand of vertices in each face and the number M of faces coming together at each vertex. If f is the number of faces, and then the total number of edges is e = (1/2)Thousand ´f, and the number of vertices is v = (1/M)K ´f. Substituting these values in Euler'due south formula f - v + eastward = 2, we notice that uncomplicated algebra leads to the equation:

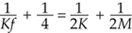
The possible solutions can be adamant quite hands. The consummate list of possible values for the pairs (K, Thou) is:

(3, 3) for the tetrahedron

(4, 3) and (3, 4) for the cube and the octahedron

(5, three) and (three, 5) for the dodecahedron and the icosahedron.

Strictly speaking, this is just the listing of genuine polyhedra satisfying the to a higher place equation. The equation does have other solutions in positive integers. These solutions correspond to then-called degenerate Ideal solidsouth, which are not bona fide polyhedra. 1 family unit of these degenerate polyhedra has K=ii and M capricious, and the other has K=ii and K arbitrary. The first example tin be idea of as a beach ball that is a sphere divided into M sections in the manner of a citrus fruit.

The Platonic solids give ascent to generalized soccer balls by a procedure known every bit truncation. Suppose we have a sharp pocketknife and slice off each of the corners of an icosahedron. At each of the 12 vertices of the icosahedron, five faces come together at a point. When we piece off each vertex, we become a small pentagon, with i side bordering each of the faces that used to see at that vertex. At the aforementioned time, we change the shape of the 20 triangles that make up the faces of the icosahedron. By cut off the corners of the triangles, nosotros turn them into hexagons. The sides of the hexagons are of two kinds, which occur alternately: the remnants of the sides of the original triangular faces of the icosahedron, and the new sides produced by lopping off the corners. The first kind of side borders another hexagon, and the second kind touches a pentagon. In fact, the polyhedron we have obtained is nil simply the standard soccer brawl. Mathematicians call it the truncated icosahedron.

Figure 8. Chopping off corners, or truncation, converts any Ideal solid into a generalized soccer ball. In detail, the standard soccer brawl is a truncated icosahedron. After truncation, the twenty triangular faces of the icosahedron become hexagons; the 12 vertices, as shown hither, plough into pentagons.

SIGANIM/Spektrum de Wissenschaft

The same truncation procedure tin can be applied to the other Platonic solids. For example, the truncated tetrahedron consists of triangles and hexagons, such that the sides of the triangles meet only hexagons, while the sides of the hexagons alternately come across triangles and hexagons. This is a generalized soccer ball with grand=three, m=3, northward=2 (and l = m ´ n = 6). The truncated icosahedron gives values for k, m and north of v, three and 2. The remaining truncations requite (k, thousand, n) = (4, 3, 2) for the octahedron, (3, iv, 2) for the cube, and (3, 5, 2) for the dodecahedron. In addition, nosotros can truncate embankment balls to obtain generalized soccer assurance with (k, one thousand, n) = (thousand, 2, 2), where one thousand tin be any integer greater than 2.

Figure 9. Generalized soccer balls autumn into 20 types. In this table, thou represents the number of sides in any black face; the product thou x n is the number of sides in any white confront. Every side of a black face meets a white face. Every nth side of a white face meets a black face. The columns b and w represent the number of blackness and white faces in the simplest representative of each blazon. For the types with n=2, every generalized soccer ball of that type is a branched roofing of the simplest 1. However, this is non truthful for other values of n. The minimal realization of type 8 is combinatorially the aforementioned equally the 2006 World Cup ball shown in Figure 2, whereas blazon ten is the standard soccer ball.

Michael Trott and Barbara Aulicino

Are these the just possibilities for generalized soccer ball patterns, or are in that location others? Over again, we tin can answer this question past using Euler's formula, f - e + v = 2. Simply as we did for the Platonic solids, we tin can express the number of faces, edges and vertices in terms of our basic data. Hither this is the number b of blackness faces, the number due west of white faces, and the parameters k, thousand and north. Now, because the number of faces meeting at a vertex is not fixed, nosotros do not obtain an equation, but an inequality expressing the fact that the number of faces coming together at each vertex is at least three. The result is a constraint on chiliad, grand and n that can be put in the following form:

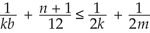
This may expect complicated, but it can easily be analyzed, only like the equation leading to the Platonic solids. It is not hard to show that north can be at most equal to half-dozen, because otherwise the left-mitt side would be greater than the right-hand side. With a footling more effort, it is possible to compile a complete list of all the possible solutions in integers thou, m and north.

Alas, the story does non cease there. In that location are some triples, such as (k, grand, n) = (four, 4, 1), that satisfy the inequality for suitable values of b but do not arise from generalized soccer assurance. However, Braungardt and I were able to decide the values of (k, m, n) that practise have realizations equally soccer assurance; these are shown in the table in Figure nine, where we too illustrate the smallest realizations for a few types. Detect that all of the ones with north=2 come from truncations of Platonic solids.

The polyhedra listed here have diverse interesting properties, of which I'll mention just ane. Besides entry ten in this tabular array, which is of grade the standard soccer ball, the tabular array contains three other fullerenes: numbers 14 and 20, and the case k=vi of entry 17. The numbers of hexagons in these examples are 30, 60 and two, respectively. (Notation that in the latter case the color scheme is reversed, then the hexagons are black rather than white.) The numbers of carbon atoms are eighty, 140 and 24, respectively. The last of these is the only fullerene with 24 atoms. In the example of 80 atoms, in that location are seven different fullerenes with disjoint pentagons, but only one occurs in our tabular array of generalized soccer assurance. For 140 atoms, in that location are 121,354 fullerenes with disjoint pentagons.

Figure 10. The tetrahedron with just 1 black confront (a) is the minimal realization of soccer-brawl type 15 in Effigy ix, where (thousand, m, n) = (3, 1, 3). Another realization, an octahedron with ii opposite blackness faces (b), is non a branched covering of a, showing that information technology is non possible to produce all generalized soccer balls with northward>2 using branched coverings.

SIGANIM/Spektrum de Wissenschaft

Braungardt and I discovered something very intriguing when we tried to see whether every generalized soccer ball comes from a branched covering of one of the entries in our table. This is true, nosotros found, for all the triples with northward=ii, that is, for generalized soccer balls for which blackness and white faces alternate effectually the sides of each white face. Withal, it is non true for other values of n! The easiest example demonstrating this failure arises for the triple (k, g, due north)= (3, 1, 3), meaning that we accept black and white triangles arranged in such a style that the sides of each black triangle meet only white ones, and each white triangle has exactly one side that meets a blackness 1. The minimal instance is just a tetrahedron with 1 face painted black (Figure 10a). Another realization is an octahedron with 2 opposite faces painted blackness (Figure 10b). This is not a branched covering of the painted tetrahedron! A branched roofing of the tetrahedron would have 3, 6, 9, … faces meeting at every vertex—only the octahedron has 4.

The reason for this foreign behavior is a subtle difference between the instance n=ii and the cases n>2. In the tetrahedron instance, there are two different kinds of vertices: a vertex at which just white faces meet, and three vertices where one blackness and two white faces see. Moreover, the painted octahedron has yet another kind of vertex. Simply in the case n=2, all the vertices look essentially the same. Every vertex has the same sequence of colors, which goes black, white, white, black, white, white, …, with only the length of the sequence left open. Thus the adjacency conditions provide a degree of command over the local structure of any generalized soccer ball with n=2. This command is defective in the due north>2 case. At nowadays, therefore, it is possible to describe all generalized soccer balls with n=two: They are branched coverings of truncated Platonic solids. Merely there is no simple way to produce all the generalized soccer balls with due north>2.

From a topologist's signal of view, spherical soccer balls are just one item example of maps fatigued on surfaces. Because the definition of soccer balls through atmospheric condition (1), (2) and (3) does not specify that soccer-ball polyhedra should be spherical, in that location is a possibility that they might also be in other shapes. Besides the sphere, there are infinitely many other surfaces that might occur: the torus (which is the surface of a doughnut), the double torus, the triple torus (which is the surface of a pretzel), the quadruple torus, etc. These surfaces are distinguished from one another by their genus, informally known as the number of holes: The sphere has genus zero, the torus has genus one, the double torus has genus two, and so on.

Figure 11. Toroidal soccer balls are of two kinds: those that are branched coverings of spherical ones, and those that are non. A branched double cover of the standard spherical soccer brawl produces a toroidal ball with 24 black and twoscore white faces (a). Opening up the standard soccer ball forth 2 edges, deforming it to a tube and and then matching the ends of the tube produces a toroidal soccer brawl with 12 black and 20 white faces (b). This pattern cannot be obtained equally a branched covering.

Soccer-brawl images were calculated and created past Michael Trott using Mathematica.

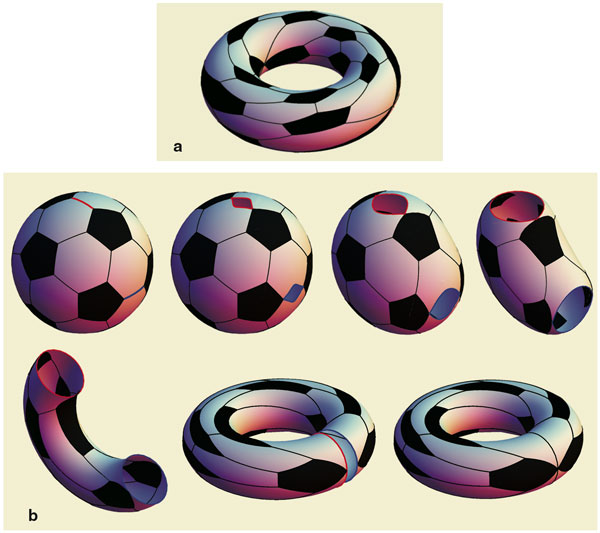
At that place are soccer balls of all genera, because every surface is a branched roofing of the sphere (in a slightly more general way than we discussed before). By arranging the branch points to be vertices of some soccer ball graph on the sphere, we tin generate soccer ball graphs on any surface. Figure 11a shows a toroidal soccer ball obtained from a 2-fold branched covering of the standard spherical ball. In this case there are four co-operative points. Notation that a two-fold branched roofing always doubles the number of pentagons and hexagons.

Hither is an easier construction of a toroidal soccer brawl. Have the standard spherical soccer ball and cutting it open forth two disjoint edges. Opening up the sphere along each cut produces something that looks rather like a sphere from which two disks have been removed. This surface has a soccer-ball blueprint on it, and the 2 boundary circles at which we have opened the sphere each have two vertices on them. If the cut edges are of the same type, significant that along both of them 2 white faces met in the original spherical soccer ball, or that along both of them a blackness face up met a white face, then we can mucilage the two boundary circles together so every bit to match vertices with vertices. (See Figure 11b for step-past-pace illustrations of this construction.) The surface built in this way is again a torus. Information technology has the structure of a polyhedron that satisfies weather (1), (2) and (three), and is therefore a soccer brawl.

This second toroidal soccer ball is not a branched roofing of the standard spherical ball, because it has the same numbers of pentagons and hexagons (12 and 20 respectively) equally the standard spherical ball. For a branched roofing these numbers would be multiplied by the caste of the covering. In this case, the failure is not caused by loss of control over the local construction of the pattern (as in the previous section), merely by a global property of the torus (the hole). Thus the basic upshot that all spherical soccer balls are branched coverings of the standard one is not truthful for soccer balls with holes.

Soccer assurance provide ample illustrations of the intimate connection that exists between graphs on surfaces and branched coverings. This circle of ideas is likewise connected to subtle questions in algebraic geometry, where the combinatorics of maps on surfaces encapsulates information from number theory in mysterious ways. Following the terminology introduced by Alexander Grothendieck, one of the leading mathematicians of the 20th century, the relevant graphs on the sphere are nowadays called dessins d'enfants.

• Braungardt, V., and D. Kotschick. 2006. The classification of football patterns. Preprint. http://129.187.111.185/~dieter/football game.pdf
• Brinkmann, Chiliad., and A. W. M. Dress. 1997. A effective enumeration of fullerenes. Periodical of Algorithms 23:345-358.
• Bundeswettbewerb Mathematik. 1988. Aufgaben und Lösungen 1983-1987. Stuttgart, Deutschland: Ernst Klett Verlag.
• • Chung, F., and Southward. Sternberg. 1993. Mathematics and the buckyball. American Scientist 81:56-71.
  • Coxeter, H. Southward. M. 1948. Regular Polytopes. London: Methuen & Co. Ltd.
  • Schneps, Fifty. (ed.). 1994. The Grothendieck Theory of Dessins d'Enfants. London Mathematical Society Lecture Annotation Serial vol. 200. Cambridge, U.K.: Cambridge University Press.
  • Yakobson, B. I., and R. E. Smalley. 1997. Fullerene Nanotubes: C_1,000,000 and Beyond. American Scientist 85:324-337.

What Size Are Hexagons In Official Soccer Ball,

Source: https://www.americanscientist.org/article/the-topology-and-combinatorics-of-soccer-balls#:~:text=Twelve%20pentagons%20and%2020%20hexagons,as%20the%20standard%20soccer%20ball.

Posted by: blackmoningeng.blogspot.com

Share this post